High-Speed Implementation of Post-Quantum Public-Key Cryptography CRYSTALS-KYBER (Introduction)

* This blog post is an English translation of an article originally published in Japanese on May 22, 2023.

Introduction

At Fixstars, we are working on a high-speed implementation of the post-quantum public key cryptosystem CRYSTALS-KYBER. We will introduce this initiative on this blog.

In this introductory part, I would like to briefly explain the mathematical background of CRYSTALS-KYBER and the concept of security in public key cryptography.

What is CRYSTALS-KYBER?

Public key cryptography is an important security technology in the information society. Public key cryptography relies on “mathematical problems that are (assumed to be) difficult to solve efficiently even with computers.” For example, RSA cryptography bases its security on the difficulty of factoring large composite numbers within a realistic timeframe. Public key cryptosystems use methods that satisfy computational security based on such “assumptions.”

However, an algorithm to solve the prime factorization problem in polynomial time using quantum computers was discovered by Peter Shor. The following article might be helpful regarding implementation experiments of Shor’s algorithm using quantum computers:
https://qiskit.org/textbook/ja/ch-algorithms/shor.html

In this context, a project led by NIST in the United States is underway to develop and standardize next-generation public key cryptography—that is, public key cryptography resistant to quantum computers. This is known as Post-Quantum Cryptography (PQC).

In the PQC project, one public key cryptosystem and three digital signature algorithms were selected as “Selected Algorithms 2022.”
https://csrc.nist.gov/Projects/post-quantum-cryptography/selected-algorithms-2022

The selected public key cryptosystem is CRYSTALS-KYBER.
Algorithm Specifications And Supporting Documentation have been published.
https://pq-crystals.org/kyber/data/kyber-specification-round3-20210131.pdf

Public Key/Digital Signature	Scheme Name	Underlying Mathematical Problem
Public Key Cryptography	CRYSTALS-KYBER	Lattice Problems
Digital Signature	CRYSTALS-DILITHIUM	Lattice Problems
Digital Signature	FALCON	Lattice Problems
Digital Signature	SPHINCS+	Hash Function Collision Search Problem

Lattice Cryptography

LWE (Learning with Errors) Problem

CRYSTALS-KYBER relies on a lattice problem called the LWE problem. KYBER has a relatively simple structure, but it might be difficult to understand by directly reading the specification. This time, I will briefly explain the LWE problem, which is its foundation.

A lattice is a set of vectors represented using an integer vector \(a\) with respect to a basis \(b\) in the vector space \(\mathbb{ R }^n\). That is, it can be expressed in the form:

\[L = \sum a_i {b_i} : a_i \in \mathbb{Z}\]

The LWE problem is divided into Search-LWE (S-LWE) and Decision-LWE (D-LWE). An adversary who can access the following instance any number of times solves the following problems:

• Search-LWE: The problem of identifying the secret vector \(s \in \mathbb{Z}_q^n\).
• Decision-LWE: The problem of distinguishing between a pair \((a, t)\) output by the instance below and a randomly sampled pair \((a’, b’)\).

Regev Cryptosystem

Public key cryptography generally consists of the following set of algorithms:

• \((pk, sk) \leftarrow Gen(params)\)
  • Takes security parameters as input and outputs a secret key sk and a public key pk.
• \(c \leftarrow Enc(pk, m)\)
  • Takes a public key pk and plaintext m as input and outputs a ciphertext c.
• \(m´ ← Dec(pk, sk, c)\)
  • Takes a public key pk, secret key sk, and ciphertext c as input and outputs a decrypted message \(m´\).
  • If decryption is successful, \(m = m´\).

Regev showed a method for constructing public key cryptosystems based on the LWE problem. This cryptosystem is called the Regev cryptosystem. The basic algorithms of the Regev cryptosystem are shown in the following diagram.

There are several variations of cryptosystems using the LWE problem. Examples include cryptosystems based on the Ring-LWE problem using polynomial rings (RLWE), and Module-LWE, which further generalizes LWE.

CRYSTALS-KYBER is one such Regev-type cryptosystem using Module-LWE.

Security of Public Key Cryptography

From here, I will explain the concept of security in public key cryptography. Public key cryptography is a particularly hot topic technologically these days, and it is considered meaningful to understand “what it means for public key cryptography to be secure.” This is a bit of a digression, but I will explain it briefly here.

Public key cryptography generally consists of the following set of algorithms:

• \((pk, sk) ← Gen(params)\)
  • Takes security parameters as input and outputs a secret key \(sk\) and a public key \(pk\).
• \(c ← Enc(pk, m)\)
  • Takes a public key pk and plaintext \(m\) as input and outputs a ciphertext \(c\).
• \(m′ ← Dec(pk, sk, c)\)
  • Takes a public key pk, secret key sk, and ciphertext c as input and outputs a decrypted message \(m′\).
  • If decryption is successful, \(m = m′\).

Here, the Dec algorithm solves the “problem” of decrypting the ciphertext to plaintext using the input information. It is necessary for Dec to have the property that:

• It can be easily executed if one possesses the secret key \(sk\).
• It cannot be easily executed if one does not possess \(sk\).

Here, “easily” is considered to mean that there exists a polynomial-time algorithm that can be executed with a sufficiently high probability.

Consider attacking the cryptosystem. The attacking entity needs to construct the following attack algorithm \(\mathscr{A}\):

> \(m” \leftarrow \mathscr{A}(pk, c)\), such that \(\mathscr{A}\) is a polynomial-time algorithm where \(m=m”\)

Public key cryptography, therefore, frames the encryption/decryption problem around a problem that is “difficult” for a Turing machine.

The security of public key cryptography is formalized by models based on mathematical games. There are various types, but I will introduce common and representative ones.

Attack Models

• CPA: Chosen Plaintext Attack; The attacker can access an oracle that encrypts arbitrary plaintexts.
• CCA: Chosen Ciphertext Attack; The attacker can access an oracle that decrypts arbitrary ciphertexts.

Furthermore, these attack models can be divided into the following two types:

• selective: Cannot use the content of past oracle accesses and their responses (like volatile memory).
• adaptive: Can use the content of past oracle accesses and their responses (like non-volatile memory).

Security Notions (Decryption Models)

• OW: One-Wayness; The entire secret information must not be leaked from the ciphertext.
• IND: Indistinguishability; Not even a single bit of secret information should be leaked from the ciphertext.

For example, for an adversary to win an IND-CCA game, it is required that not a single bit of information about the plaintext is leaked from the challenge ciphertext under a chosen ciphertext attack by the attacker. In an OW-game, it is sufficient that the plaintext cannot be directly decrypted from the ciphertext. This means that IND-security is a “stronger” form of security. Incidentally, OW-security can be derived from IND-security. In other words, if it’s IND-secure, it’s OW-secure.

CRYSTALS-KYBER is an IND-CCA-adaptive secure public key cryptosystem. This means that “even when allowed to access a decryption oracle an arbitrary number of times, referencing the decryption results each time, not a single bit of information about the secret key is leaked.”

Furthermore, in CRYSTALS-KYBER, an IND-CPA secure public key cryptosystem is constructed, then transformed into an IND-CCA-adaptive secure KEM (Key Encapsulation Mechanism) using the Fujisaki-Okamoto transformation to ensure IND-CCA2 security. Detailed algorithms are publicly available on the internet.

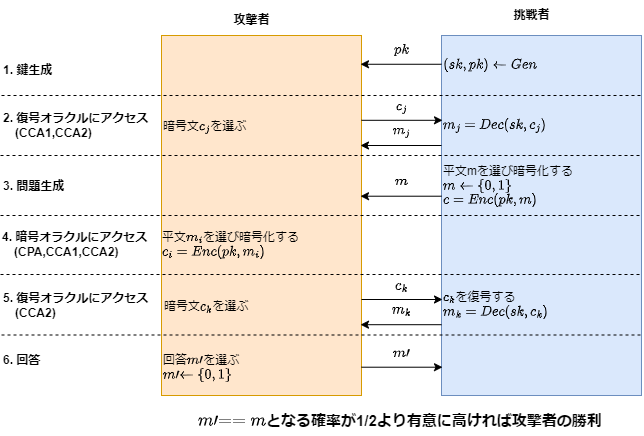
More formally, “significantly greater than 1/2” is evaluated using inequalities, where the attacker’s advantage (probability of winning the game) is bounded by a “negligible” value, often defined by a polynomial in terms of ciphertext length, etc. The attacker’s success probability is said to be “negligible”.

In the construction of a cryptosystem, proofs are required for: (1) the correctness of the cryptosystem (demonstrating mathematically that the claimed functionality is achieved by the algorithm’s inputs and outputs) and (2) the security of the cryptosystem (the security definition of the protocol and that it holds).

Conclusion

Next time, we will work on evaluating and speeding up the CPU implementation of KYBER in our project.

References

• J. Bos et al., “CRYSTALS – Kyber: A CCA-Secure Module-Lattice-Based KEM,” 2018 IEEE European Symposium on Security and Privacy (EuroS&P), London, UK, 2018, pp. 353-367, doi: 10.1109/EuroSP.2018.00032.
• Avanzi, Roberto Maria, Joppe W. Bos, Léo Ducas, Eike Kiltz, Tancrède Lepoint, Vadim Lyubashevsky, John M. Schanck, Peter Schwabe, Gregor Seiler and Damien Stehlé. “CRYSTALS-Kyber Algorithm Specifications And Supporting Documentation.” (2017).
• Moriyama, Nishimaki, Okamoto, “公開鍵暗号の数理” (Mathematics of Public Key Cryptography) (2011), Kyoritsu Shuppan.

This article was written in collaboration with intern Fujimoto-san.